Memahami RSA
Penjelasan singkat
RSA adalah singkatan dari Rivest-Shamir-Adleman, tiga peneliti dari Massachusetts Institute of Technology (MIT) yang pertama kali mempublikasikan algoritma ini pada tahun 1977. RSA merupakan salah satu algoritma kriptografi kunci publik (asimetris) pertama dan yang paling banyak digunakan hingga saat ini untuk mengamankan komunikasi data.
Fungsi utama dari RSA adalah untuk enkripsi (menyandikan data) dan otentikasi (memastikan keaslian) data. Kekuatan algoritma ini terletak pada kesulitan matematis untuk memfaktorkan bilangan besar menjadi dua bilangan prima penyusunnya.
Perbedaan mendasar RSA dengan metode enkripsi tradisional (simetris) adalah penggunaan dua jenis kunci yang berbeda namun saling berhubungan secara matematis:
Kunci Publik (Public Key): Kunci ini dapat dibagikan secara bebas kepada siapa saja. Orang lain menggunakan kunci publik kamu untuk mengenkripsi pesan yang akan dikirimkan kepada kamu.
Kunci Privat (Private Key): Kunci ini harus dijaga kerahasiaannya dan hanya diketahui oleh pemiliknya. Kunci privat digunakan untuk mendekripsi (membuka) pesan yang telah dienkripsi menggunakan kunci publik yang berpasangan dengannya.
Cara membuat kunci untuk RSA
Proses pembuatan kuncinya adalah dengan memilih dua buah bilangan prima rahasia yang sangat besar. Di bawah ini hanya sebuah contoh, di dunia nyata bilangan ini sangat besar hingga ratusan digit.
1
2
P = 7
Q = 11
P dan Q ini jangan sampai bocor, karena ini merupakan pondasi dari algoritma RSA.
Kemudian kita perlu hitung nilai N nya.
1
2
3
N = P * Q
N = 7 * 11
N = 77
Nilai N ini akan digunakan sebagai ruang lingkup dari semua perhitungan untuk melakukan enkripsi dan dekripsi. N boleh diketahui oleh publik karena meskipun orang tau N nya berapa. Sangat sulit untuk mengetahui nilai dari P dan Q nya. Seperti yang saya bilang sebelumnya, di dunia nyata 2 buah bilangan ini adalah sebuah bilang prima dengan jumlah digit mencapai ratusan digit.
Selanjutnya kita perlu menghitung nilai khusus yang disebut Euler’s Totient Function. Lambangnya yaitu $\varphi(n)$ (dibaca: phi dari n). Kita sebut aja namanya Ntot. Ntot ini rahasia ya, jangan dikasih tau orang lain ya.
Rumusnya cukup sederhana.
1
2
3
4
Ntot = (P - 1) * (Q - 1)
Ntot = (7 - 1) * (11 - 1)
Ntot = 6 * 10
Ntot = 60
Kemudian kita akan menghitung nilai e yang akan digunakan untuk membuat sebuah kunci publik. Angka ini akan berada di antara 1 dan Ntot. atau bisa ditulis $1 < e < \varphi(n)$. Biasanya sih angka yang dipilih adalah 65537. Mungkin kamu bisa membaca tentang ini. https://crypto.stackexchange.com/questions/3110/impacts-of-not-using-rsa-exponent-of-65537
Oke kita akan memilih angka di antara 1 dan 60. Angka yang kita pilih harus bilangan prima. Kemudian angka yang kita pilih juga tidak boleh memiliki faktor yang sama dengan Ntot.
Tadi kan Ntot nya 60. Lets Say kita pilih 17. Karena 17 ga bisa membagi 60 dan 17 juga merupakan bilangan prima. Alias ga bisa dibagi selain dibagi dengan 17 dan 1.
Buat yang belum tau apa itu bilangan prima. Secara sederhana nya sih gini.
Bilangan prima adalah bilangan bulat lebih dari 1 yang hanya memiliki dua faktor pembagi, yaitu 1 dan bilangan itu sendiri.
Bilangan prima paling besar yang ditemukan: https://www.sydney.edu.au/news-opinion/news/2024/11/14/mersenne-prime-number-biggest-found-search-continues.html
Kemudian kita harus menghitung nilai d yang akan digunakan untuk membuat sebuah kunci privat. Angka ini adalah sebuah invers perkalian modular dari nilai e pada Ntot. Rumus yang harus dipenuhi adalah
$(d \cdot e) \bmod \varphi(n) = 1$.
Oh iya, jika kamu belum tau apa itu modulus. Secara sederhana sih gini.
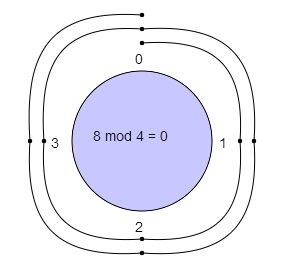
Modulus adalah hasil sisa bagi dari pembagian suatu bilangan. Misal 10 mod 7 akan menghasilkan 3. Kemudian 8 mod 4 akan menghasilkan 0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def fpb(a, b):
while b:
a, b = b, a % b
return a
def mencari_nilai_d(e, Ntot):
if fpb(e, Ntot) != 1:
return None
for i in range(1, Ntot):
if (e * i) % Ntot == 1:
return i
return None
e = 17
Ntot = 60
d = mencari_nilai_d(e, Ntot)
d = 53
Oh iya, jika kamu belum tau apa itu FPB. Secara sederhana sih gini.
FPB adalah singkatan dari Faktor Persekutuan Terbesar. FPB dari dua atau lebih bilangan adalah bilangan bulat positif terbesar yang dapat membagi habis semua bilangan tersebut. Bahasa Inggrisnya itu Greatest Common Divisor (GCD). Anjay si paling London.
Kode di atas menggunakan bruteforce untuk mencari nilai d. Meskipun mudah dipahami, cara ini tidak efisien untuk bilangan yang besar. Untuk pendekatan yang lebih efisien, kamu bisa menggunakan Extended Euclidean Algorithm.
Kodenya seperti ini:
1
2
3
4
5
6
7
8
9
10
11
12
'''
pow(base, exp, mod) dengan 3 argumen mengembalikan (base^exp) % mod
Ketika exp bernilai -1, fungsi ini akan menghitung modular multiplicative inverse
yaitu nilai yang jika dikalikan dengan base kemudian dimodulo mod akan menghasilkan 1
'''
e = 17
Ntot = 60
d = pow(e, -1, Ntot)
d = 53
Setelah melakukan beberapa perhitungan. Berikut ini adalah ringkasannya.
1
2
3
Kunci Publik: (e = 17, n = 77)
Kunci Privat: (d = 53, n = 77)
Oke, selanjutnya kita akan mencoba melakukan enkripsi dan dekripsi sebuah pesan menggunakan kunci-kunci yang sudah dibuat sebelumnya.
Enkripsi
Pesan yang kita kirimkan itu nilainya harus lebih kecil dari nilai N. Contohnya kita mau mengirimkan angka 10 deh. Rumus untuk melakukan enkripsinya adalah
\[c = m^e \pmod{n}\]1
2
3
c = 10**17 % 77
c = 100000000000000000 % 77
c = 54
54 adalah ciphertext dari hasil enkripsi menggunakan e = 17 dan n = 77.
Dekripsi
Pesan yang dienkripsi menggunakan kunci publik sebelumnya bisa kita dekripsi menggunakan rumus berikut ini:
\[m = c^d \pmod{n}\]1
2
3
m = 54**53 % 77
m = 65594778611308134080157061806172605789626085889570601355761291541899118216862184597266366464 % 77
m = 10
Hehe, berhasil kan melakukan dekripsi. Ajaib ya :D
Crack Ciphertext RSA
Misal kita diberikan sebuah ciphertext seperti ini:
1
ciphertext = [8, 119, 46, 116, 170, 179, 119, 179, 245, 209, 4, 119, 49, 245, 13, 119, 135, 49, 119, 179, 245, 209, 4, 160, 119, 223, 22]
Pesan asli dari ciphertext ini adalah sebuah kode ASCII yang bisa convert ke character normal yang bisa dibaca oleh manusia. Bagaimana cara kita melakukan dekripsinya? Kita tidak mengetahui n dan d nya.
Oh iya, jika kamu belum tau apa itu kode ASCII. Secara sederhana sih gini.
Kode ASCII (American Standard Code for Information Interchange) adalah standar pengkodean karakter yang digunakan dalam komputer dan sistem komunikasi untuk mewakili teks. ASCII menetapkan nilai numerik unik untuk setiap huruf, angka, tanda baca yang umum digunakan.
Jadi sebenarnya semua yang kita lihat di dalam komputer itu bisa direpresentasikan sebagai angka. iya dong, kan semua yang ada di komputer itu adalah binary hehe. Sebagai contoh huruf a bisa direpresentasi jadi 97.
Kamu bisa menggunakan python untuk melakukan convert dari teks ke ASCII. Tepatnya menggunakan fungsi bernama ord().
1
2
3
4
5
6
pesan = "I still love you my lover :D"
result = []
for karakter in pesan:
result.append(ord(karakter))
print(result) # [73, 32, 115, 116, 105, 108, 32, 108, 111, 118, 101, 32, 121, 111, 117, 32, 109, 121, 32, 108, 111, 118, 101, 114, 32, 58, 68]
Oke sekarang kita lanjut ke masalah sebelumnya ya, yaitu melakukan dekripsi dari ciphertext yang tidak diketahui n dan d nya.
Seperti yang kita bahas sebelumnya. Nilai N itu pasti lebih besar daripada nilai pesan yang mau dienkripsi atau didekripsi. Kita cari tau dulu nilai terbesar dari array of ciphertext tadi.
1
2
3
4
ciphertext = [8, 119, 46, 116, 170, 179, 119, 179, 245, 209, 4, 119, 49, 245, 13, 119, 135, 49, 119, 179, 245, 209, 4, 160, 119, 223, 22]
nilai_terbesar = max(ciphertext)
print(nilai_terbesar) # 245
Oke berarti kita melakukan bruteforce n dari 246. Pertama kita harus mencari tau P dan Q dari suatu N dulu.
1
2
3
4
5
6
7
8
9
10
11
12
13
def mencari_faktor_dari_n(n):
# Karena faktor dari n tidak akan lebih besar dari √n
# Buat yang belum tau pangkat 1/2 itu adalah akar dari bilangan yang dipangkatkan
max_factor = int(n**0.5) + 1
for i in range(2, max_factor):
# Jika n habis dibagi i, maka i adalah faktor dari n
if n % i == 0:
# n dibagi i dan hasilnya adalah faktor kedua
# // itu gunanya supaya hasilnya bilangan bulat. Misal 10 // 3 = 3 bukan 3.333
return i, n // i
# Jika tidak ditemukan faktor, kembalikan None aja hehe.
return None, None
Setelah kita mengetahui P dan Q dari suatu N. Kita akan mencoba mencari Ntot nya menggunakan rumus yang sama seperti sebelumnya.
1
Ntot = (P - 1) * (Q - 1)
Kemudian kita coba mencari e nya.
Note: Kode di bawah ini langsung memilih angka terkecil dari deretan angka fpb dari Ntot yang hasilnya 1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def fpb(a, b):
# Fungsi untuk mencari Faktor Persekutuan Besar (Greatest Common Divisor)
# Menggunakan algoritma Euclidean
# Berhenti jika b sudah bernilai 0 (tidak ada sisa bagi lagi)
while b:
# Tukar nilai a dan b, dimana b menjadi sisa bagi a dengan b
a, b = b, a % b
return a
def mencari_nilai_dari_e(Ntot):
# Fungsi untuk mencari nilai e (kunci publik) dari Ntot
# e harus memenuhi syarat: 1 < e < Ntot dan FPB(e, Ntot) = 1
# Loop dimulai dari 3 (bilangan ganjil pertama > 1) dengan step 2 (hanya bilangan ganjil)
for e in range(3, Ntot, 2):
# Cek apakah e dan Ntot relatif prima (FPB = 1)
if fpb(e, Ntot) == 1:
# Jika ya, maka e adalah nilai yang valid untuk kunci publik
return e
# Jika tidak ditemukan nilai e yang valid, kembalikan None
return None
Selanjutnya kita coba mencari nilai dari d nya.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def fpb(a, b):
# Fungsi untuk mencari Faktor Persekutuan Besar (Greatest Common Divisor)
# Menggunakan algoritma Euclidean
# Berhenti jika b sudah bernilai 0 (tidak ada sisa bagi lagi)
while b:
# Tukar nilai a dan b, dimana b menjadi sisa bagi a dengan b
a, b = b, a % b
return a
def mencari_nilai_d(e, Ntot):
# Fungsi untuk mencari nilai d (kunci privat) dari e dan Ntot
# d harus memenuhi syarat: (d * e) mod Ntot = 1
# Cek apakah e dan Ntot relatif prima (FPB = 1)
if fpb(e, Ntot) != 1:
# Jika tidak relatif prima, tidak ada solusi
return None
# Bruteforce mencari nilai d
for i in range(1, Ntot):
# Cek apakah (e * i) mod Ntot = 1
if (e * i) % Ntot == 1:
# Jika ya, maka i adalah nilai d yang dicari
return i
# Jika tidak ditemukan, kembalikan None
return None
Ongkeh kita udah membuat fungsi-fungsi untuk melakukan crack. Sekarang kita tinggal gabungkan kodenya.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
ciphertext = [8, 119, 46, 116, 170, 179, 119, 179, 245, 209, 4, 119, 49, 245, 13, 119, 135, 49, 119, 179, 245, 209, 4, 160, 119, 223, 22]
def decrypt_hehe(ciphertext):
nilai_terbesar = max(ciphertext)
i = nilai_terbesar + 1
def mencari_faktor_dari_n(n):
max_factor = int(n**0.5) + 1
for i in range(2, max_factor):
if n % i == 0:
return i, n // i
return None, None
def fpb(a, b):
while b:
a, b = b, a % b
return a
while True:
faktor1, faktor2 = mencari_faktor_dari_n(i)
if faktor1 is None and faktor2 is None:
i += 1
continue
Ntot = (faktor1 - 1) * (faktor2 - 1)
for e in range(3, Ntot, 2):
if fpb(e, Ntot) == 1:
for d in range(1, Ntot):
if (e * d) % Ntot == 1:
test_decrypt = [chr(c**d % i) for c in ciphertext]
# Karakter ASCII yang bisa diprint itu range nya dari 32 sampai 126
if all(32 <= ord(c) <= 126 for c in test_decrypt):
return "".join(test_decrypt)
i += 1
print(decrypt_hehe(ciphertext))
Btw kode di atas itu ga efisien ya karena bruteforce. Dalam kasus kita ini N nya itu 299 kemudian e nya 29, d nya 173. Jadi itu angka yang kecil, kalau dibruteforce bisa.
Tapi kalo kamu make script ini buat bruteforce RSA-4096. Itumah dirunning sampai alam semesta hancur, kemudian muncul lagi, kemudian hancur lagi pun belum selesai itu hehe :D
Sebenarnya bisa aja sih kita bikin kode yang isinya 2 perulangan. Jadi perulangan pertama melakukan iterasi untuk variabel n. Kemudian perulangan kedua melakukan iterasi untuk variabel d. Perulangan pertama iterasi dari nilai tertinggi dari ciphertext, mungkin berulang sampai 1000. Kemudian perulangan kedua iterasi dari 1 sampai n.
Bodohnya hari itu saya ga kepikiran karena kurang tidur :)
Mungkin kamu tertarik baca tentang algoritma Shor yang terkenal bisa crack enkripsi asimetris seperti RSA.
https://scottaaronson.blog/?p=208
Jadi output dari script di atas adalah:
1
I stil love you my lover :D
Kesimpulan
Kamu pusing ga sih? Kalau saya sih pusing hehe. Kebetulan nilai saya di mata kuliah yang berat di matematika selalu dapet kecil XD
Aduh jadi curhat nih.
Daftar link menarik: